In many physical processes, including cloud electrification, electrospray, and demulsification, droplets, and bubbles are exposed to electric fields and may either remain whole or burst in response to electrical stresses. Determining the stability limit of a droplet exposed to an external electric field has been a longstanding mathematical challenge, and the only analytical treatment to date is an approximate calculation for the particular case of a free-floating droplet.
For the first time, MIT scientists have derived the conditions under which a droplet bursts in an electric field all boil down to one simple formula. Scientists have created an equation that enables them to predict the specific strength an electric field ought to be to burst a droplet or keep it stable.
Moreover, the expectation is that the equation should help specialists tune the electric field or the size of droplets for different applications that rely upon electrifying droplets. These include innovations for air or water refining, space propulsion, and molecular investigation.
Why do liquids tend to form spherical droplets? It is a result of surface tension. Once the droplets separate from the stream of water, they assume a spherical shape, minimizing their surface area relative to their volume.
The droplet may distort from its spherical shape in the presence of other forces, such as the force from an electric field. While surface tension holds a droplet together, the electric field acts as an opposing force, pulling outward on the droplet as the charge builds on its surface.
In case if the electric field is quietly intense, the droplet becomes unable to balance the electric force, and thus, it bursts.
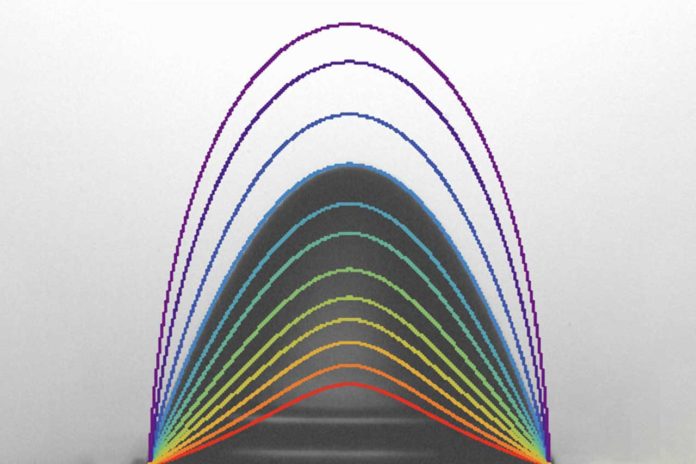
Scientists conducted an experiment in which they slowly dispensed the water droplets onto a metal plate. The metal plate was electrified to generate an electric field. Besides, a high-speed camera was used to capture the distorted shapes of each droplet.
In the wake of investigating droplets of various sizes and under different electric field strengths, scientists isolated the video frame just before each droplet burst. At that point, they outlined its critically stable shape and determined a few parameters: the droplets volume, height, and range. He plotted the information from every droplet and found that they all fell along a straight line.
Lead author Justin Beroz, a graduate student in MIT’s Departments of Mechanical Engineering and Physics, said, “From a theoretical point of view, it was an unexpectedly simple result given the mathematical complexity of the problem. It suggested that there might be an overlooked, yet simple, way to calculate the burst criterion for the droplets.”
Volume above height
Beroz explained, “For the last 100 years, the convention was to choose the height. But as a droplet deforms, its height changes, and therefore the mathematical complexity of the problem is inherent in the height. On the other hand, a droplet’s volume remains fixed regardless of how it deforms in the electric field.”
“By formulating the equations using only parameters that are ‘fixed’ in the same sense as a droplet’s volume, the complicated, unsolvable parts of the equation cancel out, leaving a simple equation that matches the experimental results.”
The new formula that scientists derived applies to three cases previously analyzed separately: a droplet pinned on a surface, sliding on a surface, or free-floating in the air. It relates five parameters: a droplet’s surface tension, radius, volume, electric field strength, and the electric permittivity of the air surrounding the droplet. Plugging any four of these parameters into the formula will calculate the fifth.
Beroz said, “Engineers can use the formula to develop techniques such as electrospraying, which involves the bursting of a droplet maintained at the orifice of an electrified nozzle to produce a fine spray. Electrospraying is commonly used to aerosolize biomolecules from a solution so that they can pass through a spectrometer for detailed analysis. The technique also produces thrust and propels satellites in space.”
“If you’re designing a system that involves liquids and electricity, it’s very practical to have an equation like this, that you can use every day.”
The results are published today in the journal Physical Review Letters. Other co-authors of the study include A. John Hart, associate professor of mechanical engineering, and John Bush, professor of mathematics.
This research was funded in part by the MIT Deshpande Center for Technological Innovation, BAE Systems, the Assistant Secretary of Defense for Research and Engineering via MIT Lincoln Laboratory, the National Science Foundation, and a Department of Defense National Defence Science and Engineering Graduate Fellowship.