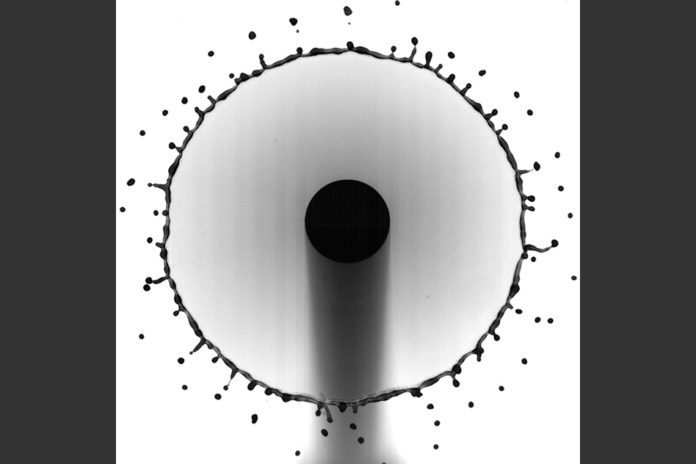
When a raindrop tumbles to the ground, it can sprinkle go down in a crown-like sheet, showering little droplets from its edge before sinking back to the surface — all in a matter of moments. MIT specialists have figured out how to track the thickness of a droplet’s edge as it sprinkles up from an assortment of surfaces.
Through this study, scientists wanted to understand spray physics and identify the key ingredients that control sprays, whether one wants to minimize secondary droplets that are undesirable or improve sprays to coat a surface homogenously. But for this, it is essential for them to know how fluids break.
Lydia Bourouiba, assistant professor of civil and environmental engineering and director of the Fluid Dynamics of Disease Transmission Laboratory at MIT, says the group’s results can be used to model the physics of sprays, such as pesticides that splash back up from crop leaves, or raindrops that may pick up and spread diseases as they bounce off contaminated surfaces.
For the past several years, Bourguiba’s group has been developing image-analysis algorithms to automatically extract and measure certain features in high-speed videos of fluid breakup processes. State-of-the-art high-speed cameras can, for the most part, capture, in slow motion, the evolution of a splashing droplet — a process that takes about several milliseconds, during which time, thousands of smaller droplets may be ejected into the air.
Researchers have utilized such rapid video recordings to quantify the extent of shot-out droplets, the thickness of the growing edge, and other sprinkle highlights, generally by hand. The algorithms can naturally recognize a sprinkling droplet’s edge and recognize it from the small drops that splash out from the edge, and the tendons that conform to the edge.
Once the calculations have prepared the image data, the specialists can obviously isolate the edge from whatever remains of the droplet’s highlights and concentrate its size at any moment amid the sprinkling procedure.
During experiments, scientists checked whether they could distinguish a typical pattern in the way a droplet’s edge develops as it sprinkles onto a surface. The analysts tried around 15 fluids of changing consistency and viscoelasticity or stringiness. They discharged single drops of every fluid from a high-accuracy “drop tower,” a setup that can control accurately the extent of the droplets discharged, the introduction of the surface underneath, and the lighting conditions in which to record the drop utilizing fast cameras.
The group discharged every droplet onto distinctive surfaces, including a pool of water, the edge of a surface, surfaces of various roughnesses, surfaces covered with a thin fluid film, and little surfaces of similar size to that of the drop, in particular rods.
After they fine-tuned the algorithms to analyze each droplet video automatically, they began to notice a pattern in the way a droplet’s rim evolved over time. The rim is typically not smooth but shows ripples and bulges.
The researchers showed that the instantaneous generation of these ripples along the rim is independent of acceleration and is instead primarily determined by the geometry of the rim. However, the rim’s thickness is related to the acceleration of the rim as it expands into the air. The greater the rim acceleration, the thinner the rim, and the more fast-moving droplets detach as it expands.
In other words, it is the rim’s acceleration that determines how much fluid remains in the rim and how much fluid is pushed out of the rim into the air, ultimately in the form of droplets.
Bourouiba said, “It’s like when one is in a car that suddenly decelerates. The deceleration of the car’s reference frame introduces a fictitious force that pushes one forward. It’s the same as what a fluid volume feels when the entire sheet decelerates.”
A key understanding the analysts had is that the difference in speeding up after some time matters. On the off chance that a swell develops more than its neighbors to wind up a lump, the prompt virtual power it feels given the momentary deceleration winds up pushing it forward more than its neighbors, bringing about its prolongation and extreme separation as a droplet.
From their trial perceptions, the group formulated a straightforward condition to foresee the thickness of a droplet’s edge given its quickening, anytime along the edge and at any moment amid the sprinkle procedure. The condition depends on what’s known as a Bond number — a nondimensional number that is normally used to contrast gravitational powers with inertial powers.
If this number is very big, gravity dominates, such as for a big puddle of water that will flatten because gravity pulls it down.
With their new equation, the researchers swapped out gravity for rim instantaneous acceleration and used the equation to calculate the Bond number — essentially, the ratio between the rim’s acceleration-induced forces and surface tension — at any point along its rim at each time.
The group found that for precarious edges, the Bond number, as they characterized it, stays equivalent to one constantly, prompting an extremely disentangled hypothetical model of the edge thickness, in spite of the multifaceted nature of this procedure that progressions consistently in time.
The group found the hypothesis holds up over a scope of viscosities, including fluids as thin as water and as thick as plasma or drain. It can likewise anticipate how the edge develops as a droplet is sprinkled onto an assortment of surfaces with various geometries.
Bourouiba says. “We showed that this new theory holds for a wide class of problems that are unsteady.”
Jose Manuel Gordillo, professor of fluid mechanics at the University of Seville in Spain, said, “The tiny droplets emitted can transport very far away from the place where the impact takes place, for instance, pathogens, or other types of organisms or molecules. I believe that these findings will not only help in the basic understanding of unsteady fragmentation of rims in natural processes but also in applications related, for instance, with printing.”
Bourouiba and her students have published their results in the journal Physical Review Letters.