In various physics and engineering applications, evaluating the properties of partial differential equations (PDEs) is essential. Traditionally, this is done using resource-intensive, high-fidelity numerical solvers.
Data-driven surrogate models offer a more efficient alternative, but they come with a significant training cost. There is a need for surrogate models with an improved balance between accuracy and cost, especially in emerging applications, when studied at scale.
MIT scientists have proposed a new method for developing data-driven surrogate models for complex physical systems in mechanics, optics, thermal transport, fluid dynamics, physical chemistry, and climate models.
This new method is known as ‘physics-enhanced deep surrogate” (PEDS).’ It combines a low-fidelity, explainable physics simulator with a neural network generator. The neural network generator is trained end-to-end to match the output of the high-fidelity numerical solver.
Raphaël Pestourie, a former MIT postdoc who is now at Georgia Tech, said, “My aspiration is to replace the inefficient process of trial and error with systematic, computer-aided simulation and optimization. Recent breakthroughs in AI, like the large language model of ChatGPT, rely on hundreds of billions of parameters and require vast amounts of resources to train and evaluate. In contrast, PEDS is affordable to all because it is incredibly efficient in computing resources and has a shallow barrier in terms of infrastructure needed to use it.”
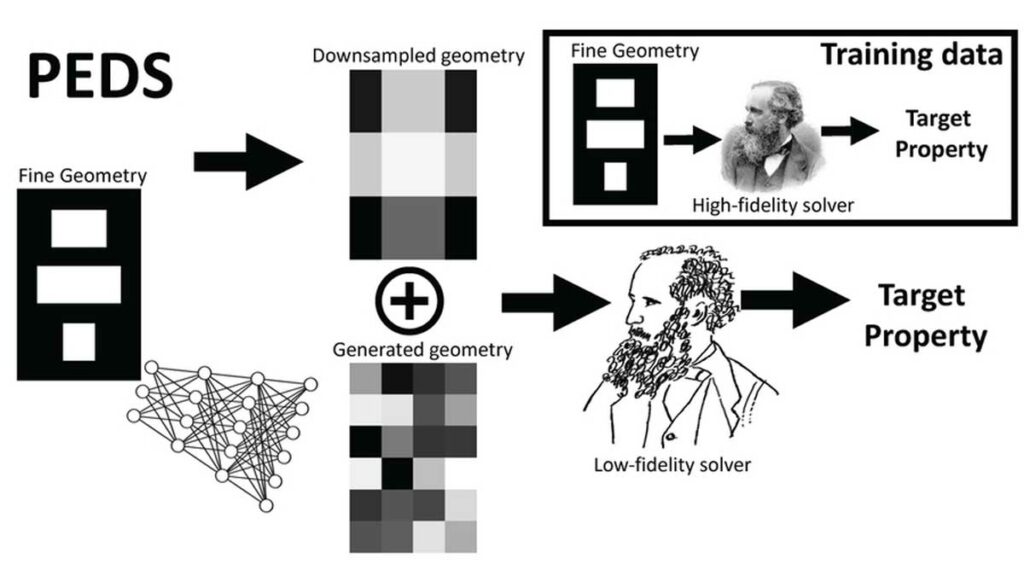
The article demonstrates that PEDS (Physics-informed Ensemble of Deep Surrogates) can achieve up to three times more accuracy than an ensemble of feedforward neural networks with limited data (around 1,000 training points). Moreover, PEDS reduces the required training data by at least a factor of 100 to reach a target error of 5 percent. Developed using the MIT-designed Julia programming language, PEDS is efficient in computation and data.
The authors emphasize that PEDS is a general, data-driven approach to connect a wide range of simplified physical models with complex systems modeled by brute-force numerical solvers. This technique offers a combination of accuracy, speed, data efficiency, and insights into the underlying biological processes.
Scientists noted, “PEDS has the potential to revive a whole body of the pre-2000 literature dedicated to minimal models — intuitive models that PEDS could make more accurate while also being predictive for surrogate model applications.”
Payel Das from the MIT-IBM Watson AI Lab and IBM Research said, “The application of the PEDS framework is beyond what we showed in this study. Complex physical systems governed by PDEs are ubiquitous, from climate modeling to seismic modeling and beyond. Our physics-inspired fast and explainable surrogate models will be of great use in those applications and play a complementary role to other emerging techniques, like foundation models.”
Journal References:
- Pestourie, Raphael, Mroueh, Youssef, Rackauckas, Chris, Das, Payel and Johnson, Steven G. 2023. “Physics-enhanced deep surrogates for PDEs.” Nature Machine Intelligence. DOI: 10.1038/s42256-023-00761-y
