The numerical solution of partial differential conditions (PDEs) is challenging due to the requirement of determining spatiotemporal features over wide length-and timescales. Often, it is computationally intractable to determine the finest features in the solution.
The only recourse is to use approximate coarse-grained portrayals, which plan to precisely represent long-wavelength dynamics while appropriately representing unresolved small-scale physics.
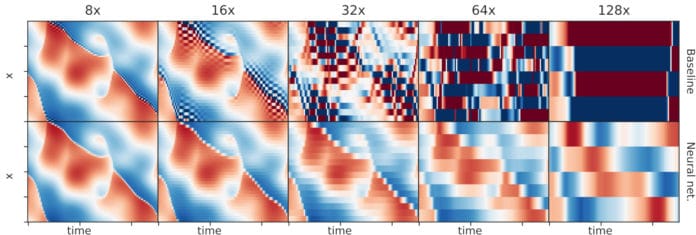
Deriving such coarse-grained equations are notoriously difficult and often ad hoc. Thus, Google engineers recently introduced a method called data-driven discretization for learning optimized approximations to PDEs based on actual solutions to the known underlying equations.
The method offers a potential way for how ML can offer continued enhancements in high-performance processing, both for solving PDEs and, all the more comprehensively, for solving hard computational problems in each sector of science.
Stephan Hoyer, Software Engineer, Google Research explained, “In our work, we’re able to improve upon existing schemes by replacing heuristics based on deep human insight (e.g., “solutions to a PDE should always be smooth away from discontinuities”) with optimized rules based on machine learning. The rules our ML models recover are complex, and we don’t entirely understand them, but they incorporate sophisticated physical principles like the idea of “upwinding”—to accurately model what’s coming towards you in a fluid flow, you should look upstream in the direction the wind is coming from.”
The study, in other words, shows a more extensive lesson about how to adequately combine machine learning and physics.
Hoyer said, “Instead of attempting to learn physics from scratch, we combined neural networks with components from traditional simulation methods, including the known form of the equations we’re solving and finite volume methods. This means that laws such as conservation of momentum are exactly satisfied, by construction, and allows our machine learning models to focus on what they do best, learning optimal rules for interpolation in complex, high-dimensional spaces.
Scientists are further planning to focus on scaling up the techniques to solve larger-scale simulation problems with real-world impacts, such as weather and climate prediction.
The details are published in the Proceedings of the National Academy of Sciences.