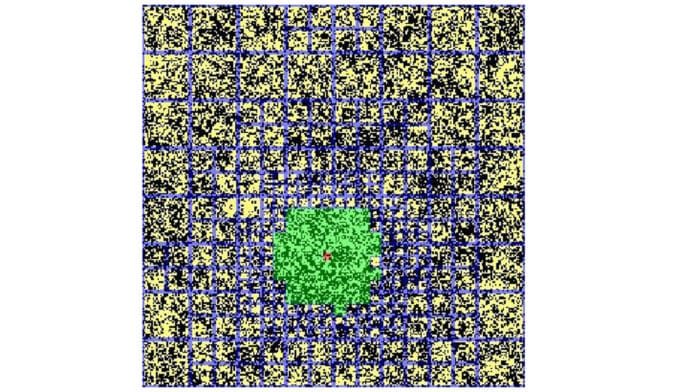
Monte Carlo algorithms explored the system’s phase space in a stochastic manner. In systems with long-range interactions among their components, Monte Carlo techniques are limited by how large a system they can explore. That is because the simulations must account for all relevant interactions, and the number of operations increases with the square of the system size. This computational challenge quickly becomes unwieldy.
Leipzig University scientists have created a highly effective approach to analyzing systems with long-distance interactions that had previously baffled specialists. These systems could be gases or even solid substances like magnets, whose atoms interact with one another and with atoms miles away.
For this purpose, scientists used Monte Carlo computer simulations. The desired attributes of the system can be ascertained from the random system states produced by this stochastic process, which was given the moniker of the Monte Carlo casino. Monte Carlo simulations offer profound insights into the physics of phase transitions in this way.
The simulations, which would have taken millennia to complete using traditional techniques, can now be conducted in a matter of days thanks to a new algorithm that the researchers have created.
When a physical system’s macroscopic characteristics, such as pressure or temperature, remain constant across time, it is said to be in equilibrium. When external changes cause a system to lose equilibrium, the system searches for a new equilibrium state, a non-equilibrium process.
Professor Wolfhard Janke said, “These processes are increasingly becoming the focus of attention for statistical physicists worldwide. While many studies have analyzed numerous aspects of nonequilibrium processes for systems with short-range interactions, we are only beginning to understand the role of long-range interactions in such processes.”
The number of operations required to determine how a short-range system evolves increases linearly with the number of components it contains for systems whose components only interact with their close neighbors. The interaction with all other components, including those located far away, must be considered for long-range interacting systems. The runtime quadratically grows as the system gets bigger.
Scientists have successfully reduced this algorithmic complexity by restructuring the algorithm and using a clever combination of suitable data structures. This drastically reduces the time needed to compute in the case of huge systems and enables the study of brand-new issues.
In systems with long-range interactions, the study demonstrates how the novel method can effectively apply nonequilibrium processes. As a result of an abrupt temperature reduction, spontaneous ordering processes in initially disordered “hot” systems are described, where ordered domains gradually expand over time until an ordered equilibrium state is obtained.
Additionally, the technique has already been successfully used by researchers at the Institute of Theoretical Physics to simulate the phase separation process, in which, for instance, two different types of particles spontaneously split. Such nonequilibrium processes are crucial to operating biological systems and industrial applications. These instances show the variety of application situations that this methodological advancement provides for both basic research and real-world applications.
Journal Reference:
- Fabio Müller et al., Fast, Hierarchical, and Adaptive Algorithm for Metropolis Monte Carlo Simulations of Long-Range Interacting Systems, Physical Review X (2023). DOI: 10.1103/PhysRevX.13.031006