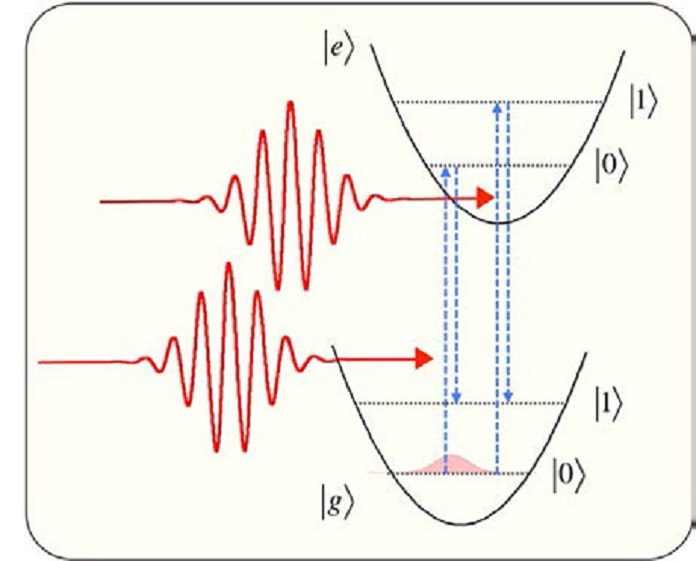
At the point when to a great degree short optical pulse enters a solid, the particles in its lattice begin vibrating. Such vibrations of molecules show both wave-like and particle-like conduct, and in quantum mechanics, these vibrations are called coherent optical phonons because they are instigated by light and oscillate in phase.
Phonons can decide different physical properties of solids, for example, thermal and electrical conductivities. In past tests, the properties of coherent optical phonons, for example, amplitude and phase, have been effectively controlled in different materials through a system called coherent control, which has been made conceivable by progress in ultrafast laser innovation.
![Amplitude control of phonon oscillation in diamond Transmittance change of the probe pulse plotted against the delay of the probe pulse with respect to the second pump pulse for five different time gaps between the two pump pulses [(a) to (e)]. The spikes are caused by the overlapping of the probe pulse with the first or second pump pulse. The change in amplitudes of the sinusoidal waves after the second set of spikes confirms that the coherent control of phonons is realized by varying the time gap.](https://www.techexplorist.com/wp-content/uploads/2018/06/Amplitude-control-of-phonon.jpg)
Transmittance change of the probe pulse plotted against the delay of the probe pulse with respect to the second pump pulse for five different time gaps between the two pump pulses [(a) to (e)]. The spikes are caused by the overlapping of the probe pulse with the first or second pump pulse. The change in amplitudes of the sinusoidal waves after the second set of spikes confirms that the coherent control of phonons is realized by varying the time gap.
Now, scientists at the Tokyo Institute of Technology in collaboration with Professor Yutaka Shikano at Quantum Computing Center, Keio University and Institute for Quantum Studies, Chapman University have detailed a hypothetical structure that basically and practically clarifies the age and discovery of coherent optical photons.
The hypothesis depends on a model including two conditions of electrons and additionally the quantum harmonic oscillator, one of only a handful couple of quantum-mechanical systems for which a correct arrangement is known. Calculations relying on this hypothesis demonstrated that the amplitude of a controlled phonon can be communicated by the whole of two sinusoidal capacities.
During an experiment, scientists used diamond as the coherent control of its optical phonons is promising to develop quantum memory. The coherent control is accomplished by utilizing two immensely short laser beams, known as pump pulses: one pulse induces an oscillation, or phonons, while alternate controls the amplitude of oscillation.

The points in the two figures show the experimentally measured amplitude and phase of the phonon oscillation with respect to the time gap between the two pump pulses. The points are consistent with the solid lines in the two figures, which represent the predictions of the proposed theory.
The time gap between the two pulses is shifted to control the properties of the produced phonons. A probe pulse sent with a delay after the two pump pulses is used to quantify the properties of the produced phonons by identifying changes in the transmitted force of this heartbeat concerning the delay.
The measured amplitude and phase of controlled oscillations incited by the direct pulses in diamond demonstrated a striking concurrence with the predictions of the hypothesis. Along these lines, an exhaustive comprehension of the coherent control of coherent optical phonons has been accomplished. This hypothesis is required to be helpful in the improvement of memory frameworks for quantum figuring, notwithstanding different applications in electronics, optics, materials science, and superconductivity.
The measured amplitude and phase of controlled oscillations induced by the pump pulses in diamond showed a remarkable agreement with the predictions of the theory. Thus, a comprehensive understanding of the coherent control of optical phonons has been achieved. This theory is expected to be useful in the development of memory systems for quantum computing, in addition to other applications in electronics, optics, materials science, and superconductivity.
The authors of the study include Hiroya Sasaki, Riho Tanaka, Yasuaki Okano, Fujio Minami, Yosuke Kayanuma, Yutaka Shikano, and Kazutaka G. Nakamura. The study is detailed in the journal Scientific Reports.